Problem:
Detection of a-priori unknown substructure which are almost isometric modulo the 3-D rigid motion group.< >

Problem definition:
Given A known Database of molecules, each as a set ( linearly ordered, or not) of  points representing Atoms , and given a new Molecule M: Find all the molecules Mi in the DB, and  rigid Transformations Ti : R3 ->  R3  so that a matching from ( a part of ) the Atoms of M to those of Mi will give an RMSD (root mean square distance) bellow a given limit L.

Applications:

•    structural comparison of proteins
•   receptor ligand docking

Examples

• 1dgaC - 1svy :

• 1tt1 - 1tf1:

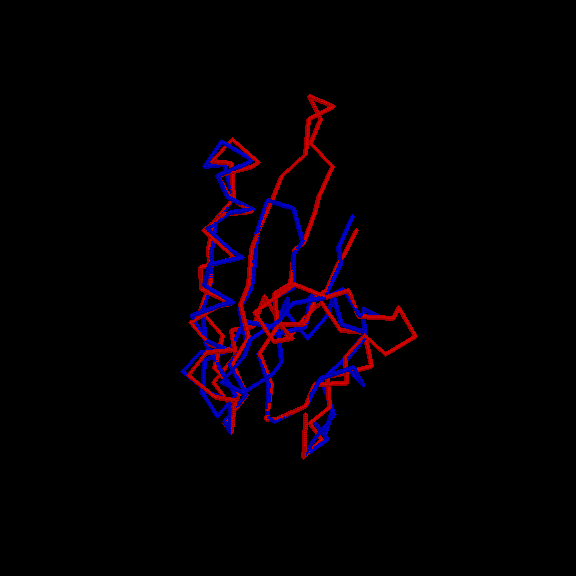
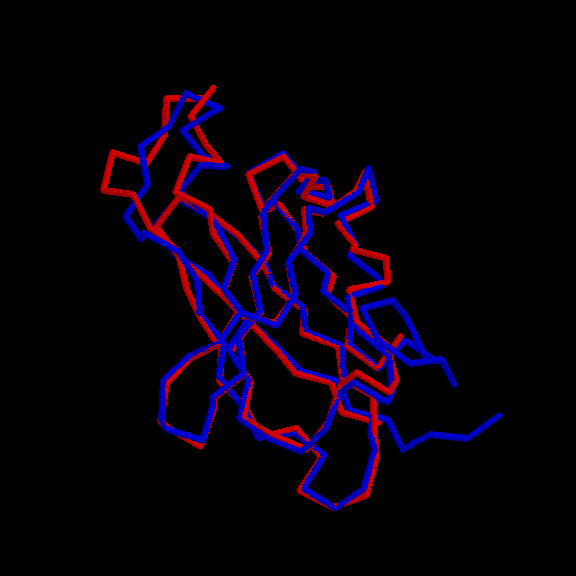
Back to Index.
 

Geometric Hashing:

the 2D case:

• Preprocessing stage:

For each model (2D "molecule") we iterate on all pairs of its points ("Atoms") .

For each basis pair we:
Compute the associated frame of reference.
For each point in each model we:
Compute its coordinates in the above frame of reference Use the coordinates as a key for inserting an Entry to a Hash table.
The Entry will include:
{
Model name.
Frame of Reference ( the basis pair, not the f.o.r. itself)
Identity of point in model
}
The complexity of this stage is O( N³ * M) where M is the number of models and N the number of points in each model.
This stage requires no knowledge of the "Scene" (the input "molecule") and can be done off line.
 
• Recognition stage:

Given a scene:
For each ordered pair of points:
Compute the unique frame of reference.
For each point in scene:
compute its coordinates in the above frame of reference, and look up any entries in the hash table under these coordinates.
These entries represent points that match the above scene point under the given transformation. For each entry found:
check if the basis pair in it is consistent:
if so, "cast a vote" (raise a counter) for the pair (model,f.o.r.) and match the point on the scene to the point in the model.
After finishing going through the basis pairs, cluster the highest - ranking matches by transformation.
For each cluster:
calculate the transformation (by a least RMSD criterion) given from all matched basis pairs .
For each model:
Extend the match list (if you took only a part of the scene for the preceding stages) ,i.e. take the model, map it point by point to the scene under the calculated transformation, add all consistent matches to the match list.
give (model, Transformation [,match list]) as output.

To reduce the complexity , we can :

1. take only triplets that are not 'too small' ( for numeric reasons) or 'too big' ( these have less chance of appearing in an a molecule with a partial match to the input).
2. In the case of linear polymers (which is the dominant case in biological macro-molecules) we can use the linearity , and look only at triplets which are in the right order in the sequence, or even give some heuristic ( such as Ci , Ci+2 , Ci+4  , for example, or like taking the C_a , C , and N atoms from each amino acid.) that will reduce the complexity to linear ( at the risk of losing some potential solutions).

Since these features usually have at least several dozens of Amino Acids, using them , plus all the "unrelated" C_a atoms can reduce the input size in 1-2 orders of magnitude, thus greatly cutting both the worst case and the mean time complexity.
Back to Index.

The Problem of Non rigid bodies, specifically rotary joints:

Molecules , when they bond with other molecules, tend to change their shape.
In some cases, these changes can be approximated with rotational movements around fixed hinges.
This gives us ( C.S. people) the motivation to try and solve the above problem(s) with an option for movements of parts of the molecule around fixed hinges.
So, if we have some prior information we can try and give an answer for the molecule matching problem that will have better correspondence  to the biological (wanted) solution.

Statement of Problem:
Given a database of known molecules, each represented as a (possibly linearly ordered) set of points in R³ and possible rotary joints , and an input molecule ( "scene") find the best (set of) choice of:
Molecule in the DB , Rigid transformation and a set of rotations ( on the chosen molecule's joints) ,such that the chosen molecule, under the transformation and the bending of joints, will match the input molecule most closely.

We are interested in a Scheme that will "vote" for consistent parts of a molecule together, not as different pieces, since this would cut down Post processing, and improve the quality of the solution (we can lower the bound, which means more possible answers.)

Let us look in the simple case of one hinge first: in this case, we have 2 moving parts.
For each (un-occluded) part, there is a rigid Transformation from the model to the scene, that gives us the part's (invariant) frame of reference.
Also, in this local frame of reference, the translation from the origin to the axle is invariant.
This gives us the motivation to use local f.o.r.s (basis triplets) and vote for quartets {model, part, axle, f.o.r.}.

Again , we have 2 stages to the algorithm:

• Preprocessing stage:

for each part we iterate on all basis triplets of its points.
For each basis triplet we:
Compute the associated frame of reference.
Compute the translation to the Axle (No need for rotation...)
For each point in part we:
Compute its coordinates in the above frame of reference
Use the coordinates as a key for inserting an Entry to a Hash table.
The Entry will include: {
Model name. (if more then one Model)
Part Name.
Frame of Reference
Translation (of f.o.r) to Axle.
Identity of point in model
}
The complexity of this stage is O( N⁴) where N is the number of points in each part.
Again, this stage requires no knowledge of the "Scene" and is done off line.
• Recognition stage:

Given a scene:
For each ordered triplet of points (in a "small enough" region):
Compute the unique frame of reference.
For each point in scene:
Compute its coordinates in the above frame of reference, and look up any entries in the hash table under these coordinates.
For each entry found:
check if the basis triplet and the Axle in it are consistent with the scene: if so , "cast a vote" (raise a counter)  for the quartet  (model, part, axle, f.o.r.) and match the point in the scene to the point in the model.
After finishing going through the triplets, cluster the highest - ranking matches by transformation and Axle.
For each cluster ,calculate the transformation (by a least RMSD criterion) given from all matched triplets.
For a specific part, Extend the match list (if you took only a part of the scene for the preceding stages).

give (model, part, Transformation [match list]) as output.

As before, Extending the match list simply means this:
For each part of the recognized  model:

take each point (not already matched) and transform its coordinates, then check in the input for a point with "close enough" coordinates: when (an unmatched) one is found, match it to the one in the model.
The complexity of this stage is O(S⁴) where S is the number of points in the scene.
The generalization to the case of a linear chain of parts is obvious, but the generalization to the case where we have several hinges on the same part or several parts on the same Axle (some general "graph") give rise to questions of weighting, i.e. the same triplet should vote to several hinges, should its vote be the same as a triplet voting for only 2 Axles? for 1 ?

This is done for a single model, but can just as easily be done for M models in a DB, where the complexity of both the preprocessing and the recognition stages (assuming a good hash table)  will be linear in M.
Also ,the above method will work in the special case of no bending of joints, so that "limited over jointing" will not stop from identifying the wanted model.The last remark is cautious, since fixing a joint in a molecule means that a lot of the ("non local") basis triplets will not be entered to the hash table and therefore will not influence the identification, so that "greatly over jointing", will cause the algorithm to function poorly.