There are several physical and chemical forces that interact between
the two molecules. These forces are used to define various docking scores
that measure how good is each solution. These scores take into account
the strength of these forces and the plausibility of the docking solution.
The most significant forces are:
The contact surface is defined as the surface where the distance between
the molecules is smaller than a given threshold.
Notice that we shall usually try to achieve a contact surface which
is "large enough" instead of "maximal" and that we usually try to maximize
not the size of the contact surface but a score measuring the quality of
the proposed docking solutions. These two parameters are correlated but
are not equivalent.
Back to Index.
The DOCK algorithm (Kuntz et al.)
The basic version of this algorithm was developed by Kuntz et al. at
the university of california over 15 years ago and, despite its age, is
still considered to be a successful method for solving the rigid docking
problem and is used as a reference point to other algorithms.
The algorithm is rather slow and thus has difficulties in handling
large surface. Therefore it is primarily used in solving ligand-protein
docking while trying to focus on 'interesting' sites on the surface of
the molecules.
-
Compute the molecular surface using Connolly's method. The output of this
stage is a set of points on the 'smoothed' molecular surface with their
normals.
-
SPHGEN (Sphere Generator) - This stage creates a new representation of
the molecular surface of the protein and the ligand using 'pseudo-atoms'
(see below) and then uses this representation to find plausible docking
sites on the molecular surface - these docking sites that SPHGEN is looking
for are cavities in the surface of the receptor. The rest of the algorithm
focuses on these sites only.
This stage is crucial to the success of the algorithm and will be explained
in more detail below.
SPHGEN consists of the following stages:
(I) For each pair on Connolly points pi,pja
sphere passing through this pair is placed such that its center is on one
of the points normal (see Fig.2).
Remember that each pi is a point on the surface of
a specific atom of one of the molecules.
We now define Snorm(i) = {Spheres that their center is
on the normal of pi}
(II) Assuming there are n Connolly
points, then for each 1<=i<=n and pi is
on the surface of the receptor, we throw away all the spheres in Snorm(i)
and leave only the one with the smallest radius. This throws all the spheres
that penetrate the surface of the receptor.
(III) Leave only the spheres where Theta
< 90o (see Fig.2). Otherwise
the points that define the sphere, pi and pj,
are too close to each other and therefore are not located in a cavity on
the receptor's surface.
(IV) For each atom, leave only the sphere
with the maximal radius. This step leaves only the spheres that 'touch'
the surface of the atom.
(V) If the points that define the sphere,
pi
and pj, belong to two different atoms, and the distance
between these atoms on the molecular sequence is less than 4 - discard
the sphere. This is done because the length of a curve on an Alpha-helix
is 3.6 and we wish not to treat these sites as possible docking sites.
The remaining spheres are called pseudo-atoms.
The next stage looks for clusters of intersecting pseudo-atoms. The
existence of this kind of cluster indicates the existence of a cavity in
the molecular surface, which is considered to be a good docking site.
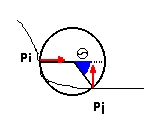 Figure 2 - Two
points pi and pj on the Connolly surface
with their normals (in red). The sphere in this figure is in Snorm(i)
because
its center is on pi's normal. The angle Theta
is marked in blue.
Figure 2 - Two
points pi and pj on the Connolly surface
with their normals (in red). The sphere in this figure is in Snorm(i)
because
its center is on pi's normal. The angle Theta
is marked in blue.
After all this is performed on the receptor the same is done on the
ligand, but this time we take the points and the vectors opposite to their
normals, in order to create the spheres inside the surface instead of outside
the surface.
The result of SPHGEN on the receptor is sometimes called the 'negative
image' and on the ligand it's called the 'positive image'.
-
Matching - For each docking site, the algorithm tries to find a transformation
T
that would give a good correspondence between the centers of the pseudo-atoms
of the protein to those of the ligand (in some cases, the centers of the
real atoms of the ligand are used, instead of the centers of its pseudo-atoms).
In some versions of DOCK, clusters of pseudo-atoms are separated into
sub-clusters in order to improve the complexity of this stage. One way
of doing this is to discard the largest sphere in the cluster, which sometimes
causes the cluster to be divided into two sub-clusters (see
Fig.3).
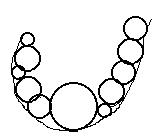 Figure 3 - An
example of a cluster of pseudo-atoms outside the receptor's Connoly surface.
If we will remove the largest pseudo-atom (here in the middle of the cluster)
we would have two sub-clusters of pseudo-atoms
Figure 3 - An
example of a cluster of pseudo-atoms outside the receptor's Connoly surface.
If we will remove the largest pseudo-atom (here in the middle of the cluster)
we would have two sub-clusters of pseudo-atoms
The matching problem
In the matching problem of rigid docking we are trying to find a translation
and rotation of one molecule, such that good matching between the interesting
points in both molecules is formed.
In Kuntz's group the distances between the point used instead of the
points locations: For each molecule, the receptor (R) and the ligand
(L), an apropriate distance matrix is defined - dRi,j
and dLi,j, respectively. They then try to
find two subsets in R and L such that their distances will
be the same, with some tolerance of error. These two subsets define two
subgraphs with almost similar distances between their vertices.
This is done using a method similar to the interpretation tree
by Grimson and Lozano-Perez:
The root has several mathcing candidates and as we go down in the tree
we should check that the distances on the path comply with the required
tolerance of error. In order to have a more efficient algorithm, Kuntz's
group implementation trims off paths where the matching is not good enough,
but this implementation become sensitive to the order of the points in
the tree, therefore the algorithm could have an exponential run-time.
Another way of solving the matching problem is to find a "large enough"
clique in a matching graph. If we have n points in the receptor
and m point in the ligand, the matching graph has n*m vertices
where each vertex represents a point from the receptor and a point from
the ligand.
Let G=(V,E) be the mathcing graph and let u,v be vertices
in V where u represents uL and uR
(points in the ligand and the receptor, respectively) and v represents
vL
and vR . An edge e=(u,v) will be added to E
only when ABS [dL(uL,vL) - dR(uR,vR)]
< tolerance. Therefore, a clique in the matching graph defines subsets
of points in the ligand and the receptor with similar distances.
Evaluating the match
In order to evaluate the quality of the match a score is calculated.
The score should take into account the size of the contact surface between
the molecules and should not allow one molecule to penetrate the other.
The DOCK algorithm uses a cubic grid that fills the binding site and
every cell in this grid has a score according to its distance from the
centers of the receptor's atoms:
-
1 if the distance is 2.8A
- 4.5A.
-
-127 if the distance is less than 2.8A.
-
0 if the distance is more than
4.5A.
(In some cases the distance 2.8A is replaced by 2.4A)
For each proposed transformation, the poisition of the ligand's points
(i.e. the centers of its atoms or pseudo-atoms) in the grid are calculated
and the score is calculated as the sum of scores of these points.
Additional scores were used in several versions of the algorithm - for
example, in one version a Van der-Vaals energy score was calculated to
the transformations that had a good matching scores.
There were also attemps to refin the matching using molecular dynamics,
but this has not proved as a good method until now. A possible reason is
that during the docking process, several atoms in both molecules change
their position slightly.
Back to Index.
Soft (flexible) Docking
We shall now descibe shortly the principles of two soft docking algorithms.
Jiang & Kim
An enumeration on the 6-dimensional space of rigid transformation is
performed and these transformations are given score according the their
energetic value. Both molecules are placed on a grid and the matching is
evaluated using the distances between grid cells, the number of penetrations
and the directions of the points' normals. The algorithm works on the output
of Connolly's algorithm and works on the entire molecular surface (i.e.
no cavities are looked for - as opposed to the DOCK algorithm).
In order to decrease the enumeration, the algorithm uses two resolutions
- low and fine. The low resolution uses ~0.3 points per square angstrem,
and the fine resolution uses ~1 point per square angstrem.
Each cell in the grid is marked as "surface" (if it contains at least
one Connolly point) or "volume" (if it doesn't contain any Connolly point).
Usually, each surgace cell contains 2-3 Connolly points.
An enumeration on the rotations of one of the molecules (usually smaller
one) is performed. For each rotations:
-
Calculate the surface and volume cells of the molecule.
-
Assuming that there's at least one pair of surface cells (one from each
molecule) that are matched be the transformation, an enumeration on all
of these pairs is performed. For each pair the transformation is calculated
and it is evaluated by checking the directions of the normals, the number
of surface-to-surface matches and the number of penetrations.
-
The good transformations are those who have a small number of penetrations
and a lot of surface-to-surface matches.
This is done first in low resolution and the best results are calculated
again in fine resolution with the addition of an approximated energetic
score. The approximated enrgetic score is calculated according to the number
of "favourable" and "unfavourable" interactions. There are several categories
for the atoms of each molecule and combinations of these categories are
marked as "favourable" if they have a good contribution to the enrgetic
plausibilty of the match, or "unfavourable" otherwise.
For example, it is unfavourable that an atom with positive charge is
placed near another atom with positive charge, but it is favourable if
two atoms are adjacent if one of them is an H-donor and the other is an
H-acceptor.
Katchalski-Katzir et al. (1992)
The basic idea is to enumerate on the possible translations, while
using FFT to calculate the matching score efficiently. Similar to the previous
algorithm, both molecules are placed on a 3-dimensional grid, but here
3 types of grid cells are defined - "volume", "surface" and "intermediate".
If the molecules are A and B, we define the matrices
Al,m,n
and Bl,m,n as follows (l,m,n are the grid coordiantes)
Al,m,n = { 1 - if (l,m,n) is a "surface" cell,
q - if (l,m,n) is an "intermediate" cell, 0 - otherwise }
Bl,m,n = { 1 - if (l,m,n) is a "surface" cell,
r - if (l,m,n) is an "intermediate" cell, 0 - otherwise }
We choose q<0 and r>0 while |q| is large and
|r| is small. The scalar product of these matrices can be efficiently
calculated using FFT thus improving the algorithms performace considerably.