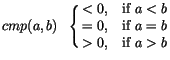An instance L of the parameterized data type list<E> is a sequence of items
(list_item). Each item in L contains an element of data type E, called
the element type of L. The number of items in L is called the length of L.
If L has length zero it is called the empty list. In the sequel <x> is
used to denote a list item containing the element x and L[i] is used to
denote the contents of list item i in L.
| int |
L.length() |
returns the length of L. |
| int |
L.size() |
returns L.length(). |
| bool |
L.empty() |
returns true if L is empty, false otherwise. |
| list_item |
L.first() |
returns the first item of L (nil if L is empty). |
| list_item |
L.last() |
returns the last item of L. (nil if L is empty) |
| list_item |
L.get_item(int i) |
returns the item at position i (the first position is 0).
Precondition: 0 <= i < L.length(). Note that this takes
time linear in i. |
| list_item |
L.succ(list_item it) |
returns the successor item of item it, nil if
it=L.last().
Precondition: it is an item in L. |
| list_item |
L.pred(list_item it) |
returns the predecessor item of item it, nil if
it=L.first().
Precondition: it is an item in L. |
| list_item |
L.cyclic_succ(list_item it) |
| |
|
returns the cyclic successor of item it, i.e.,
L.first() if it = L.last(), L.succ(it) otherwise. |
| list_item |
L.cyclic_pred(list_item it) |
| |
|
returns the cyclic predecessor of item it, i.e,
L.last() if it = L.first(), L.pred(it) otherwise. |
| void |
L.remove(E x) |
removes all items with contents x from L.
Precondition: compare has to be defined for type E. |
| E |
L.contents(list_item it) |
returns the contents L[it] of item it.
Precondition: it is an item in L. |
| E |
L.inf(list_item it) |
returns L.contents(it). |
| E |
L.front() |
returns the first element of L, i.e. the contents
of L.first().
Precondition: L is not empty. |
| E |
L.head() |
same as L.front(). |
| E |
L.back() |
returns the last element of L, i.e. the contents
of L.last().
Precondition: L is not empty. |
| E |
L.tail() |
same as L.back(). |
| int |
L.rank(E x) |
returns the rank of x in L, i.e. its first
position in L as an integer from [1...|L|]
(0 if x is not in L). Note that this takes
time linear in rank(x). Precondition: compare has to be
defined for type E. |
| list_item |
L.push(E x) |
adds a new item <x> at the front of L and
returns it (L.insert(x,L.first(),LEDA::before)). |
| list_item |
L.push_front(E x) |
same as L.push(x). |
| list_item |
L.append(E x) |
appends a new item <x> to L and returns
it (L.insert(x,L.last(),LEDA::after)). |
| list_item |
L.push_back(E x) |
same as L.append(x). |
| list_item |
L.insert(E x, list_item pos, int dir=LEDA::after) |
| |
|
inserts a new item <x> after (if dir=LEDA::after)
or before (if dir=LEDA::before) item pos into L and
returns it (here LEDA::after and LEDA::before
are predefined constants).
Precondition: it is an item in L. |
| E |
L.pop() |
deletes the first item from L and returns its contents.
Precondition: L is not empty. |
| E |
L.pop_front() |
same as L.pop(). |
| E |
L.Pop() |
deletes the last item from L and returns its contents.
Precondition: L is not empty. |
| E |
L.pop_back() |
same as L.Pop(). |
| E |
L.del_item(list_item it) |
deletes the item it from L and returns its contents L[it].
Precondition: it is an item in L. |
| E |
L.del(list_item it) |
same as L.del_item(it). |
| void |
L.erase(list_item it) |
deletes the item it from L.
Precondition: it is an item in L. |
| void |
L.move_to_front(list_item it) |
| |
|
moves it to the front end of L. |
| void |
L.move_to_rear(list_item it) |
| |
|
moves it to the rear end of L. |
| void |
L.move_to_back(list_item it) |
| |
|
same as L.move_to_rear(it). |
| void |
L.assign(list_item it, E x) |
| |
|
makes x the contents of item it.
Precondition: it is an item in L. |
| void |
L.conc(list<E>& L1, int dir = LEDA::after) |
| |
|
appends (dir = LEDA::after or prepends
(dir = LEDA::before) list L_1 to list L and
makes L_1 the empty list.
Precondition: : L != L_1 |
| void |
L.swap(list<E>& L1) |
swaps lists of items of L and L1; |
| void |
L.split(list_item it, list<E>& L1, list<E>& L2) |
| |
|
splits L at item it into lists L1 and L2. More precisely,
if it != nil and L = x_1,...,x_k-1,it,x_k+1,...,x_n
then L1 = x_1,...,x_k-1 and L2 = it,x_k+1,...,x_n. If
it = nil then L1 is made empty and L2 a copy of L. Finally
L is made empty if it is not identical to L1 or L2.
Precondition: it is an item of L or nil. |
| void |
L.split(list_item it, list<E>& L1, list<E>& L2, int dir) |
| |
|
splits L at item it into lists L1 and L2. Item it
becomes the first item of L2 if dir==LEDA::before and the
last item of L1 if dir=LEDA::after.
Precondition: it is an item of L. |
| void |
L.apply(void (*f)(E& x)) |
for all items <x> in L function f is
called with argument x (passed by reference). |
| void |
L.reverse_items() |
reverses the sequence of items of L. |
| void |
L.reverse_items(list_item it1, list_item it2) |
| |
|
reverses the sub-sequence it1,...,it2 of items of L.
Precondition: it1 = it2 or it1 appears before it2 in L. |
| void |
L.reverse() |
reverses the sequence of entries of L. |
| void |
L.reverse(list_item it1, list_item it2) |
| |
|
reverses the sequence of entries L[it1] ... L[it2]. |
| void |
L.permute() |
randomly permutes the items of L. |
| void |
L.permute(list_item* I) |
permutes the items of L into the same order as stored in the
array I. |
| void |
L.clear() |
makes L the empty list. |
| void |
L.sort(int (*cmp)(E, E ), int dd=1) |
| |
|
sorts the items of L using the ordering defined
by the compare function cmp : Ex E -> int,
with
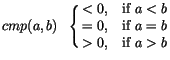
More precisely, if (in_1,...,in_n) and
(out_1,...,out_n) denote the values of L
before and after the call of sort, then
cmp(L[out_j], L[out_j+1]) <= 0 for
1<= j<n and there is a
permutation
pi of [1..n] such that out_i = in_pi_i for
1 <= i <= n
. |
| void |
L.sort() |
sorts the items of L using the default ordering of type E,
i.e., the linear order defined by function
int compare(const E&, const E&). |
| void |
L.merge_sort(int (*cmp)(E, E )) |
| |
|
sorts the items of L using merge sort and the ordering
defined by cmp. The sort is stable, i.e., if x=y and
<x> is before <y> in L then <x> is before
<y> after the sort. merge_sort is more efficient than
L.sort() if L contains large pre-sorted intervals. |
| |
() |
as above, but uses the default ordering of type E. |
| void |
L.bucket_sort(int i, int j, int (*f)(E )) |
| |
|
sorts the items of L using bucket sort,
where f : E -> int with f(x) in [i..j] for
all elements x of L. The sort is stable,
i.e., if f(x)=f(y) and <x> is before <y> in
L then <x> is before <y> after the sort. |
| void |
L.bucket_sort(int (*f)(E )) |
| |
|
same as bucket_sort(i,j,f) where i and j are the
minimal and maximal value of f(e) as e ranges over
all elements of L. |
| void |
L.merge(list<E>& L1, int (*cmp)(E, E )) |
| |
|
merges the items of L and L1 using the ordering defined by
cmp. The result is assigned to L and L1 is made empty.
Precondition: L and L1 are sorted incresingly according to the
linear order defined by cmp. |
| |
(list<E>& L1) |
merges the items of L and L1 using the default linear
order of type E. |
| void |
L.unique(int (*cmp)(E, E )) |
| |
|
removes duplicates from L.
Precondition: L is sorted incresingly according to the ordering
defined by cmp. |
| |
() |
removes duplicates from L.
Precondition: L is sorted incresingly according to the default
ordering of type E. |
| list_item |
L.search(E x) |
returns the first item of L that contains x,
nil if x is not an element of L.
Precondition: compare has to be defined for type E. |
| list_item |
L.min(int (*cmp)(E, E )) |
returns the item with the minimal contents with respect
to the linear order defined by compare function cmp. |
| |
() |
returns the item with the minimal contents with respect
to the default linear order of type E. |
| list_item |
L.max(int (*cmp)(E, E )) |
returns the item with the maximal contents with respect
to the linear order defined by compare function cmp. |
| |
() |
returns the item with the maximal contents with respect
to the default linear order of type E. |
| void |
L.read(istream& I, char delim = (char)EOF) |
| |
|
reads a sequence of objects of type E terminated
by the delimiter delim from the input stream I
using operator>>(istream&,E&).
L is made a list of appropriate length and the
sequence is stored in L. |
| void |
L.read(char delim = '
 n n |
calls L.read(cin, delim) to read L from
the standard input stream cin. |
| void |
L.read(string s, char delim = '
 n n |
| |
|
As above, but uses string s as a prompt. |
| void |
L.print(ostream& O, char space = ' ') |
| |
|
prints the contents of list L to the output
tream O using operator<<(ostream&,const E&)
to print each element. The elements are separated by
character space. |
| void |
L.print(char space = ' ') |
calls L.print(cout, space) to print L on
the standard output stream cout. |
| void |
L.print(string s, char space = ' ') |
| |
|
As above, but uses string s as a header. |
| list<E>& |
L = L1 |
The assignment operator makes L a copy of
list L_1. More precisely if L_1 is the sequence
of items x_1, x_2, ... , x_n then L is made a
sequence of items y_1, y_2, ... , y_n with
L[y_i] = L_1[x_i] for 1 <= i <= n. |
| E& |
L[list_item it] |
returns a reference to the contents of it. |
| list_item |
L[int i] |
an abbreviation for L.get_item(i). |
| list_item |
L += E x |
same as L.append(x); returns the new item. |
| ostream& |
ostream& out << L |
same as L.print(out); returns out. |
| istream& |
istream& in >> list<E>& L |
same as L.read(in)); returns in. |
The data type list is realized by doubly linked linear lists. All operations
take constant time except for the following operations: search and rank take
linear time O(n), item(i) takes time O(i), bucket_sort takes time
O(n + j - i) and sort takes time O(n* c*log n) where c is the
time complexity of the compare function. n is always the current length of
the list.